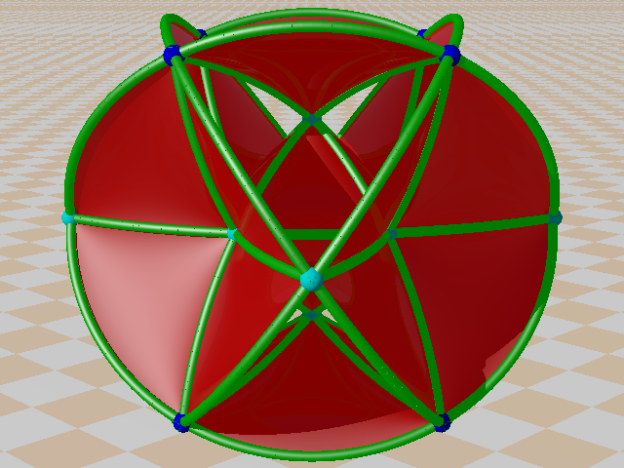
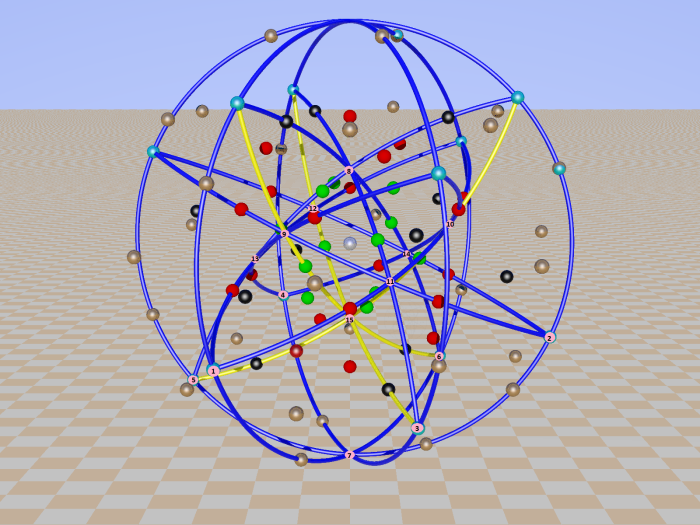
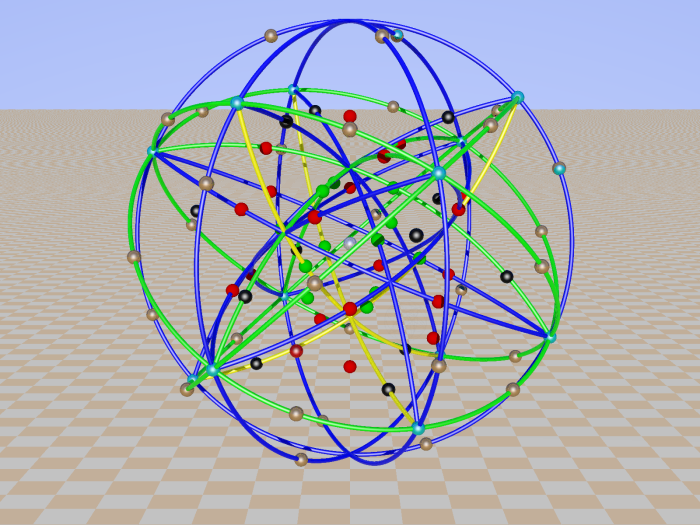
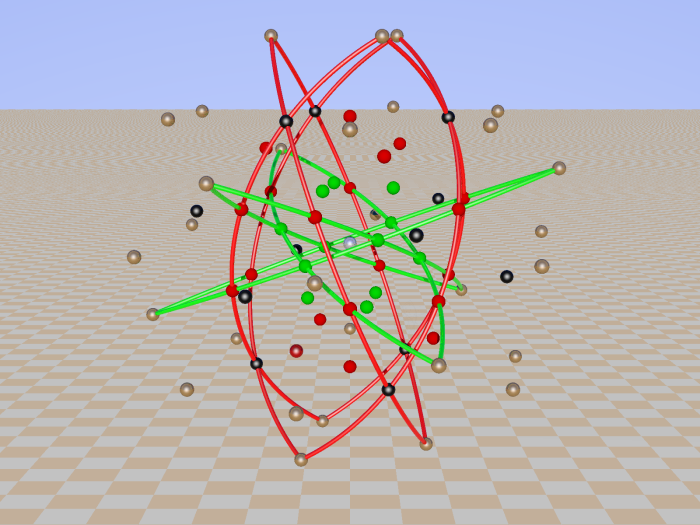
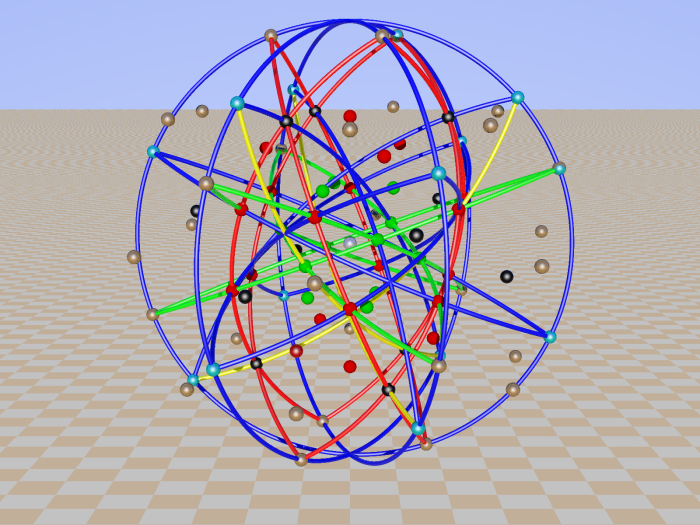
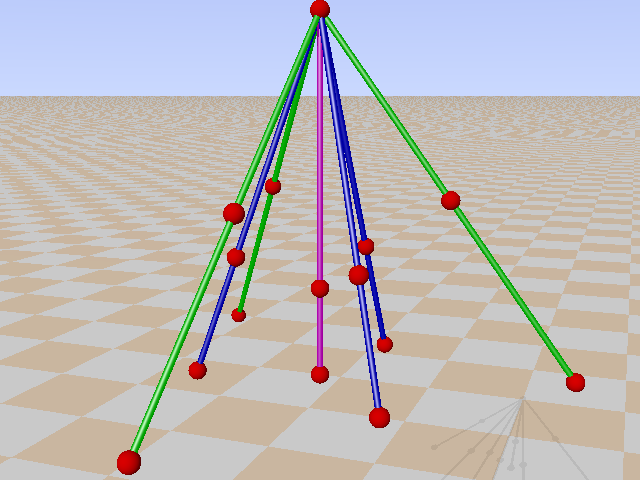
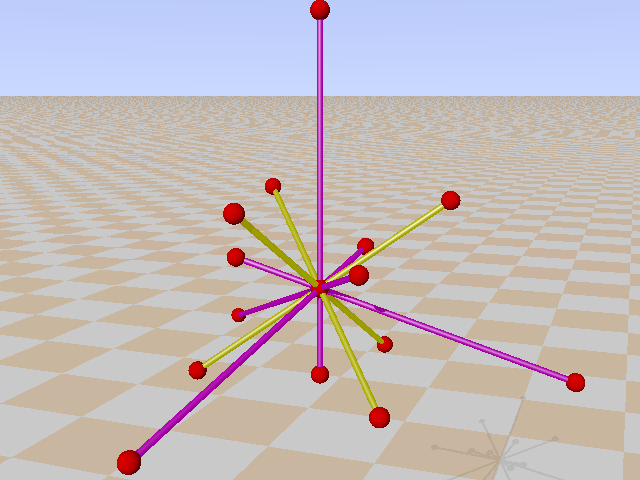
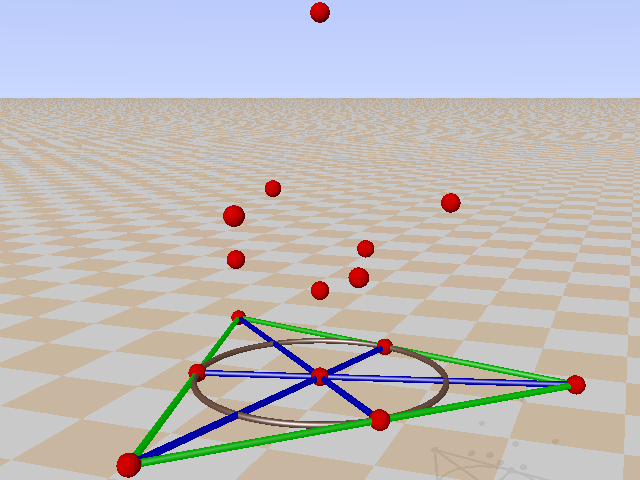
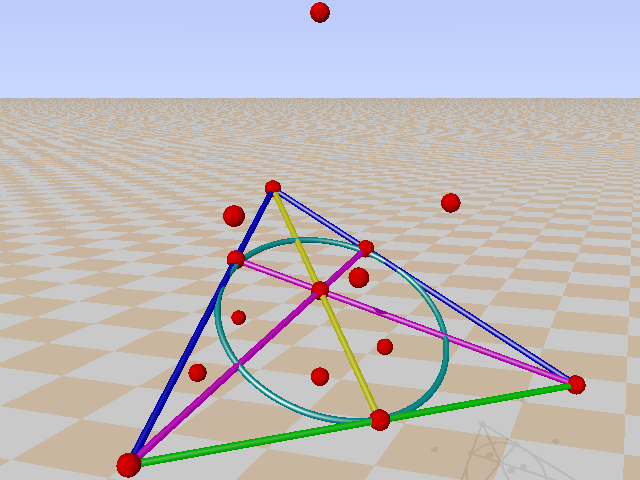
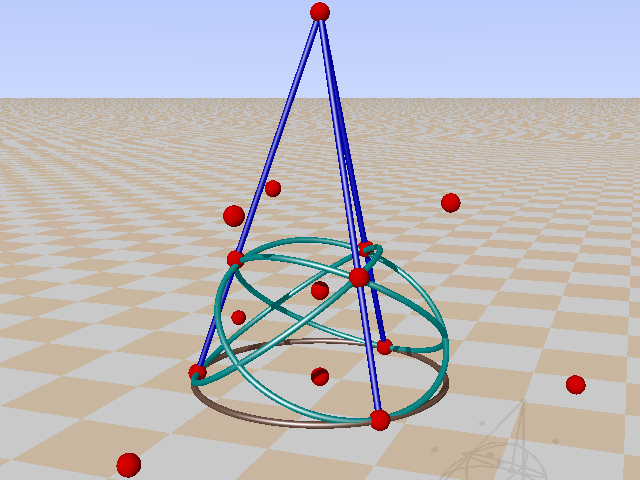
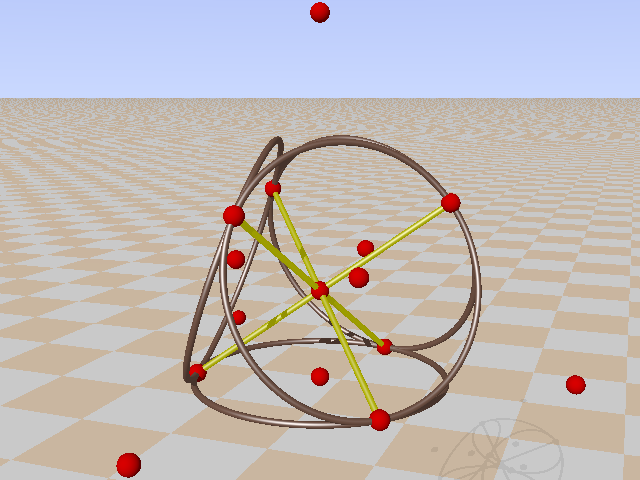
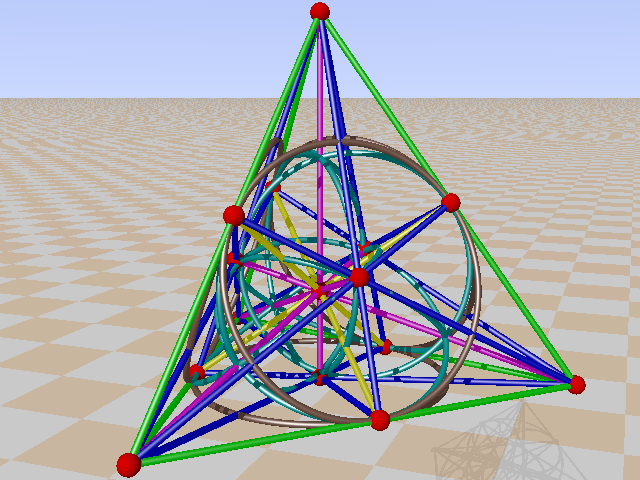
In the Cayley-Salmon configuration, complement of GQ(2,2), one can trace six configurations equivalent to a Mermin pentagram. Points on the Klein quadric are lines in PG(3,2).
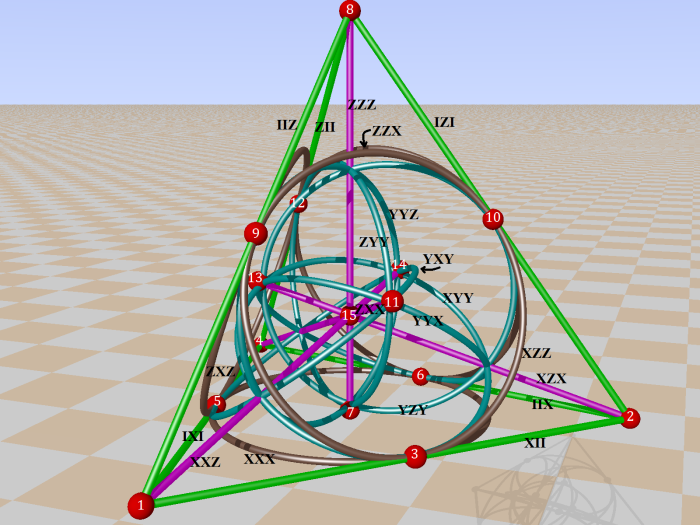
In the next 6 pictures they are selected:
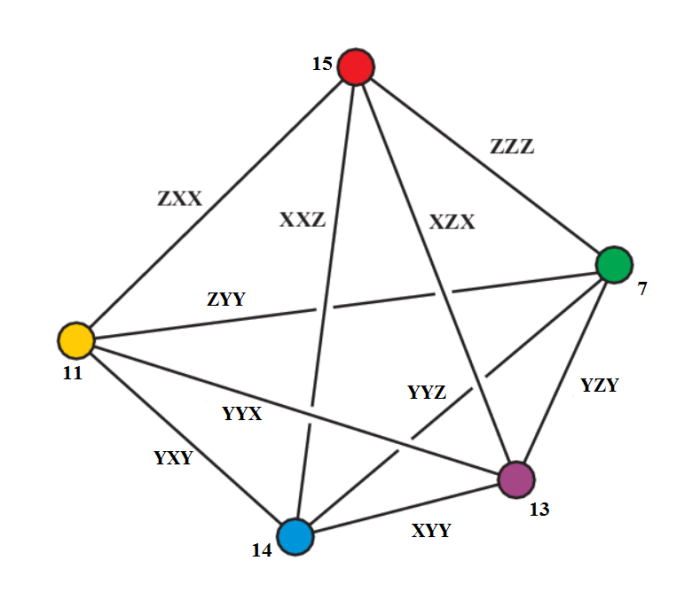
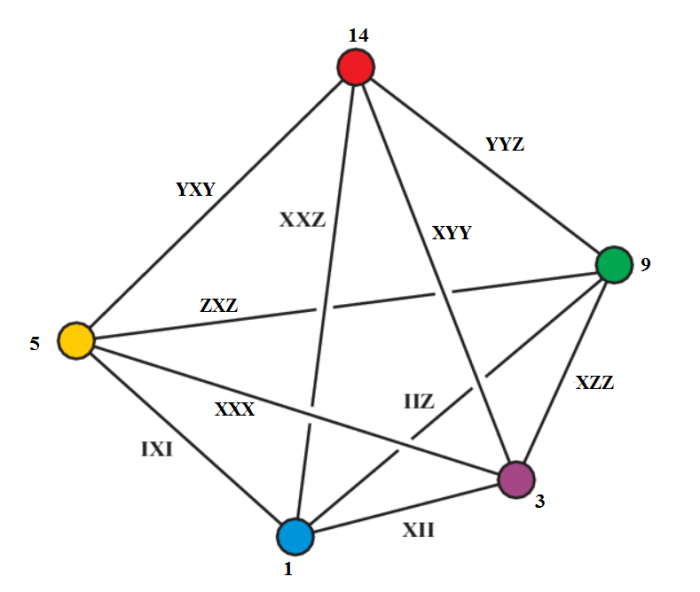
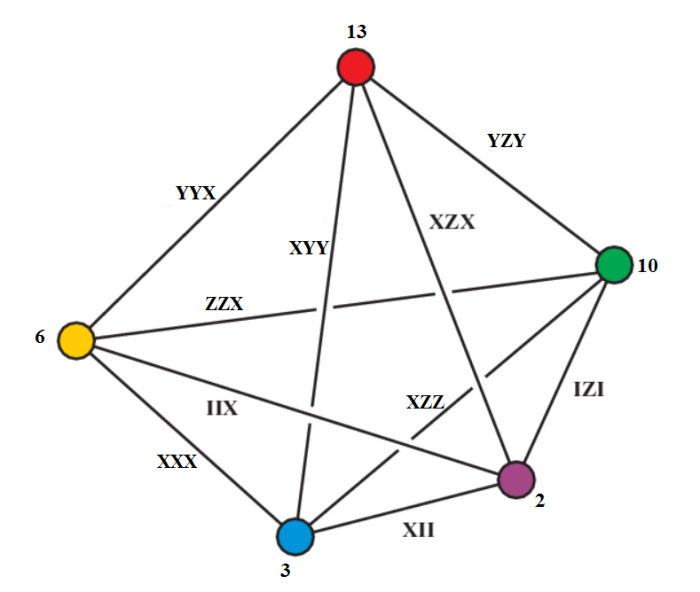
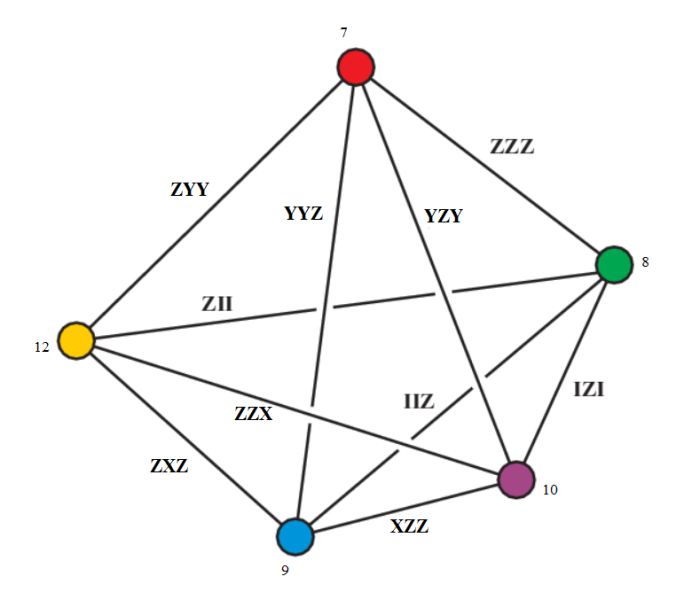
I
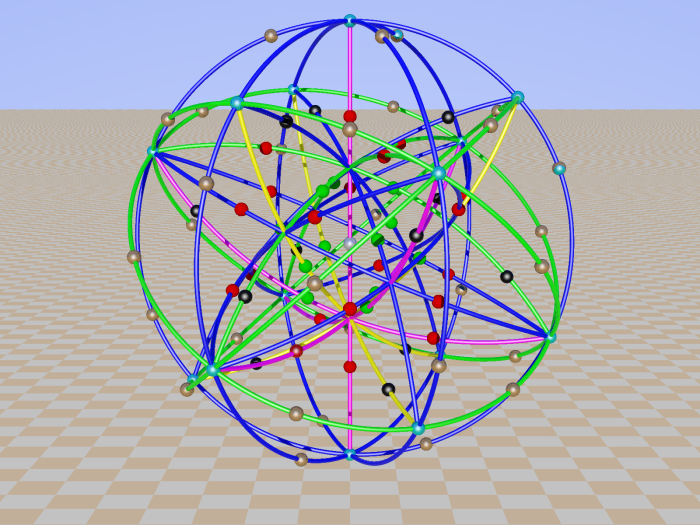
If one choose for planes with four lines instead of pencils of four lines we get Desargues configurations, complement of Petersen graph. Three examples:
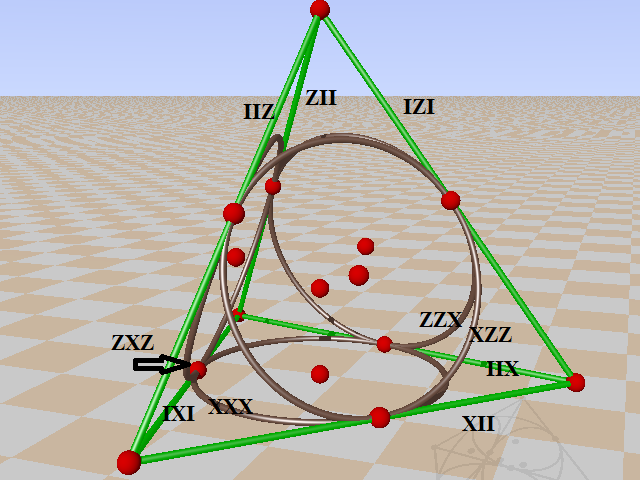
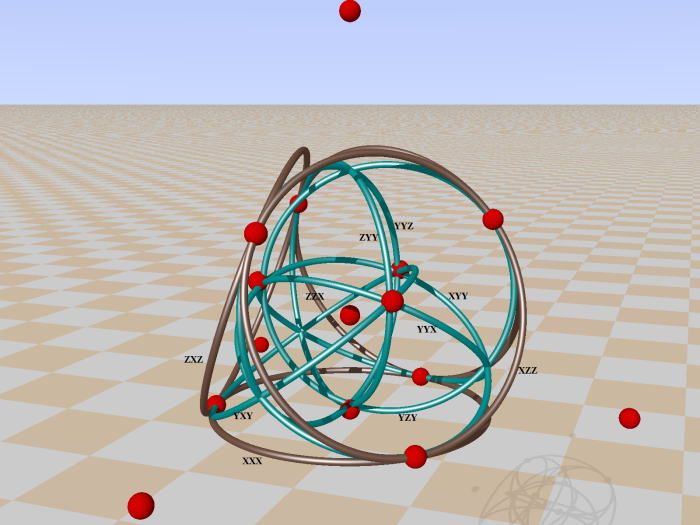
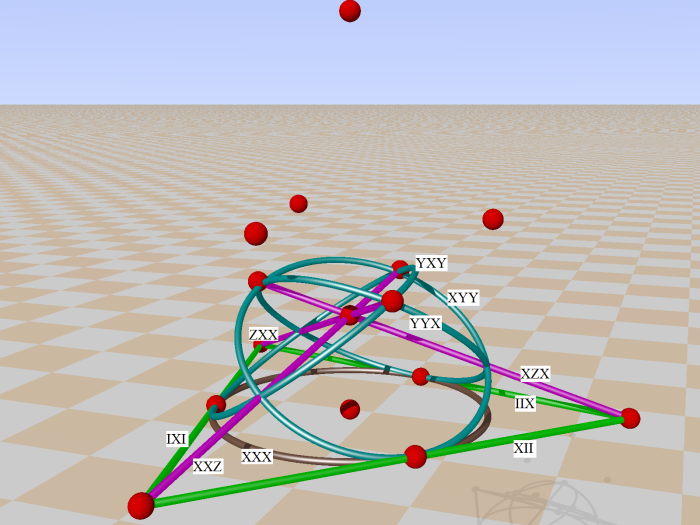
By symmetry you can find the remaining three from the the last one.
Levay and Szabo discuss the Magic Veldkamp Line (MVL) in
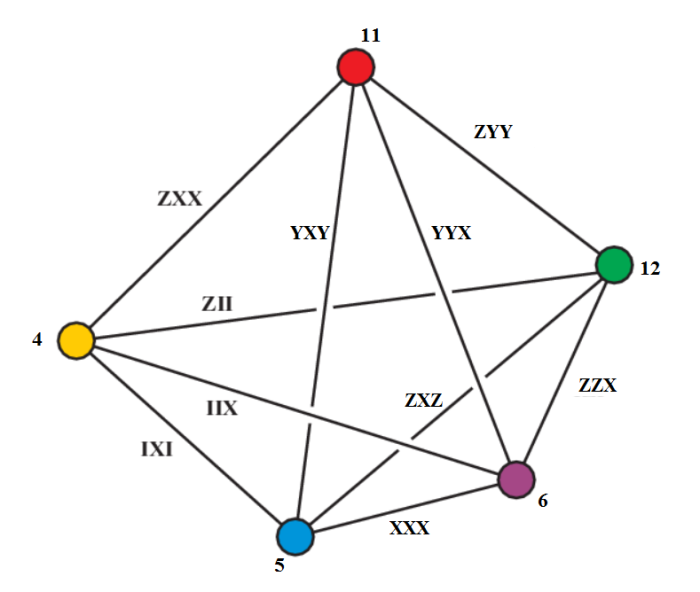
The last picture for instance shows five planes with four lines
XXX XII IXI IIX
XXX XYY YXY YYX
IXI YXY ZXX XXZ
YYX ZXX XZX IIX
XYY XII XZX XXZ
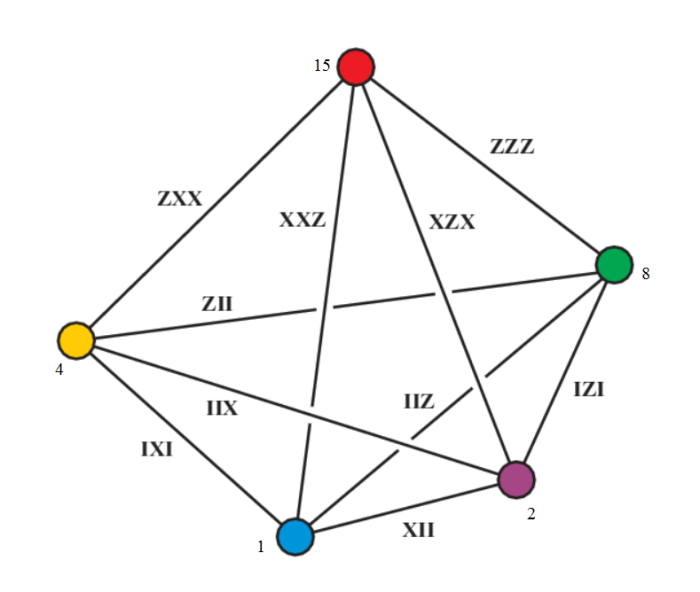
The five planes in PG(3,2) are the 5 lines of a Mermin pentagram. The core of the MVL is made up of 15 elements that are the lines of the GQ below:
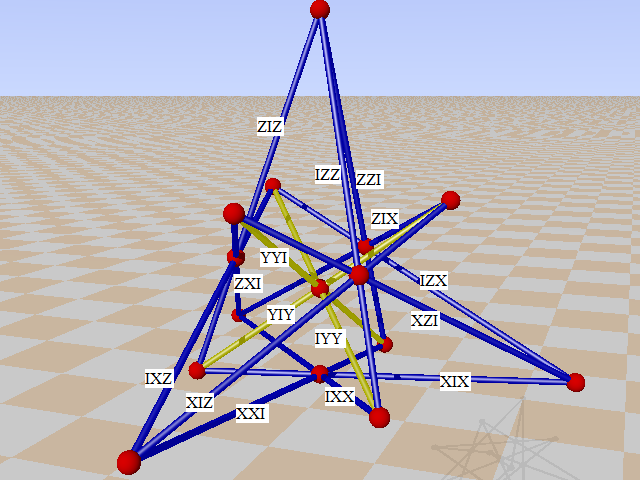
The Lagrangian subspaces correspond to maximal sets of pairwise commuting three-qubit Pauli operators. They are fano planes. They are found by completing the planes in PG(3,2) with the flat pencils of the GQ.
XXX XII IXI IIX IXX XIX XXI
XXX XYY YXY YYX IZZ ZIZ ZZI
IXI YXY ZXX XXZ XIZ ZIX YIY
YYX ZXX XZX IIX XZI ZXI YYI
XYY XII XZX XXZ IZX IXZ IYY
Spreads in the points of the GQ in PG(5,2) correspond to ovoids in PG(3,2). Call the six ovoids of the GQ A,B,C,D,E,F. Then mark the points by membership of the ovoids.
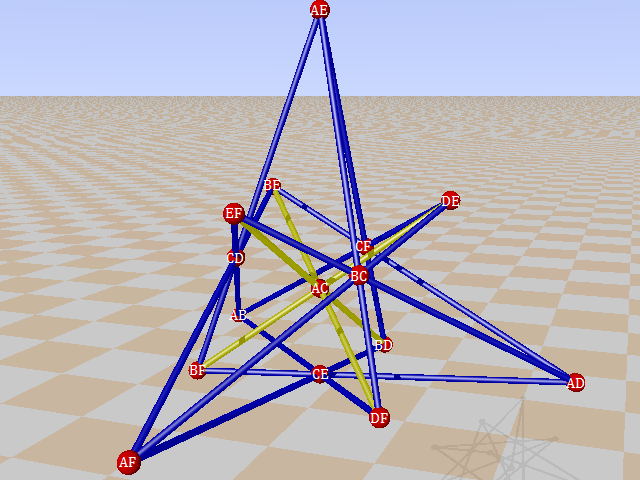
We see that the five added flat pencils are pencils through the five points of ovoid E.
This is the Mermin pentagram with flat pencils through points of ovoid A (FIGURE 9):
YZY ZZX ZYY YYX XIZ IXZ XXI AF
YZY XZZ XYY YYZ ZIX IXX ZXI AB
ZXZ ZZX XZZ XXX YIY IYY YYI AC
ZXZ ZYY YXY YYZ XIX IZX XZI AD
XXX XYY YXY YYX ZIZ IZZ ZZI AE
This is the Mermin pentagram with flat pencils through points of ovoid B:
YZY XZZ XYY YYZ ZIX IXX ZXI AB
XII XZZ IZI IIZ XIZ IZZ XZI BC
XXZ ZZZ YYZ IIZ YYI ZZI XXI BD
XYY XII XZX XXZ IZX IYY IXZ BE
YZY XZX IZI ZZZ YIY XIX ZIZ BF
This is the Mermin pentagram with flat pencils through points of ovoid C (FIGURE 8):
XII XXX IXI IIX XIX IXX XXI CE
ZXZ XXX XZZ ZZX YIY IYY YYI AC
XII XZZ IZI IIZ XIZ IZZ XZI BC
ZXZ IXI ZII IIZ ZIZ IXZ ZXI CD
ZZX IZI ZII IIX ZIX IZX ZZI CF
This is the Mermin pentagram with flat pencils through points of ovoid D:
ZXZ ZYY YXY YYZ XIX IZX XZI AD
ZXZ IXI ZII IIZ ZIZ IXZ ZXI CD
ZII ZXX ZZZ ZYY IXX IYY IZZ DF
XXZ ZZZ YYZ IIZ YYI ZZI XXI BD
IXI YXY ZXX XXZ YIY XIZ ZIX DE
This is the Mermin pentagram with flat pencils through points of ovoid F:
YZY ZZX ZYY YYX XIZ IXZ XXI AF
ZZX IZI ZII IIX ZIX IZX ZZI CF
ZII ZXX ZZZ ZYY IXX IYY IZZ DF
YZY XZX IZI ZZZ YIY XIX ZIZ BF
YYX ZXX XZX IIX XZI ZXI YYI EF
The six pentagrams of the PG(3,2)-pencils of figure 2 to 7 are conjugate to the six pentagrams of the PG(3,2)-planes. I will write down the twelve pentagrams and the 15 flat pencils occuring twice in 2 ovoids. The ovoids in the middle and the conjugate pentagrams at the left and right.
A ( {7-11-13-14-15} figure 9, [1-2-4-8-15] figure 2 ):
XXXI {14} YZY ZZX ZYY YYX XIZ IXZ XXI IXI XXZ XII IIZ [1] IIIZ
XIXX {11} YZY XZZ XYY YYZ ZIX IXX ZXI IXI ZXX ZII IIX [4] IZII
XXXX {15} ZXZ ZZX XZZ XXX YIY IYY YYI XZX XXZ ZXX ZZZ [15] ZZZZ
XXIX {13} ZXZ ZYY YXY YYZ XIX IZX XZI XZX XII IZI IIX [2] IIZI
IXXX {7} XXX XYY YXY YYX ZIZ IZZ ZZI ZZZ ZII IZI IIZ [8] ZIII
B ( {4-5-6-11-12} , [4-5-6-11-12] figure 7 ):
XIXX {11} YZY XZZ XYY YYZ ZIX IXX ZXI IXI ZXX ZII IIX [4] IZII
IXII {4} XII XZZ IZI IIZ XIZ IZZ XZI ZII ZXX IXI IIX [11] ZIZZ
IXXI {6} XXZ ZZZ YYZ IIZ YYI ZZI XXI ZZX XXX IIX YYX [6] IZZI
XXII {12} XYY XII XZX XXZ IZX IYY IXZ ZII ZYY ZXZ ZZX [12] ZZII
IXIX {5} YZY XZX IZI ZZZ YIY XIX ZIZ IXI ZXZ YXY XXX [5] IZIZ
C ( {1-2-4-8-15} figure 8, [7-11-13-14-15] figure 3 ) :
XIII {8} XII XXX IXI IIX XIX IXX XXI ZYY ZZZ YZY YYZ [7] IZZZ
XXXX {15} ZXZ XXX XZZ ZZX YIY IYY YYI XZX ZZZ ZXX XXZ [15] ZZZZ
IXII {4} XII XZZ IZI IIZ XIZ IZZ XZI ZYY ZXX YXY YYX [11] ZIZZ
IIXI {2} ZXZ IXI ZII IIZ ZIZ IXZ ZXI XZX YZY XYY YYX [13] ZZIZ
IIIX {1} ZZX IZI ZII IIX ZIX IZX ZZI XXZ YXY XYY YYZ [14] ZZZI
D ( {2-3-6-10-13}, [2-3-6-10-13] figure 5 ):
XXIX {13} ZXZ ZYY YXY YYZ XIX IZX XZI XZX XII IZI IIX [2] IIZI
IIXI {2} ZXZ IXI ZII IIZ ZIZ IXZ ZXI XZX YZY XYY YYX [13] ZZIZ
IIXX {3} ZII ZXX ZZZ ZYY IXX IYY IZZ XYY XZZ XXX ZII [3] IIZZ
IXXI {6} XXZ ZZZ YYZ IIZ YYI ZZI XXI ZZX XXX IIX YYX [6] IZZI
XIXI {10} IXI YXY ZXX XXZ YIY XIZ ZIX YZY IZI XZZ ZZX [10] ZIZI
E ( {7-8-9-10-12}, [7-8-9-10-12] figure 6):
XIII {8} XXX XII IXI IIX IXX XIX XXI ZZZ ZYY YZY YYZ [7] IZZZ
IXXX {7} XXX XYY YXY YYX IZZ ZIZ ZZI ZZZ ZII IZI IIZ [8] ZIII
XIXI {10} IXI YXY ZXX XXZ XIZ ZIX YIY YZY IZI XZZ ZZX [10] ZIZI
XIIX {9} YYX ZXX XZX IIX XZI ZXI YYI IIZ XZZ XZX YYZ [9] ZIIZ
XXII {12} XYY XII XZX XXZ IZX IXZ IYY ZII ZYY ZXZ ZZX [12] ZZII
F ({1-3-5-9-14}, [1-3-5-9-14] figure 4 ):
XXXI {14} YZY ZZX ZYY YYX XIZ IXZ XXI IXI XXZ XII IIZ [1] IIIZ
IIIX {1} ZZX IZI ZII IIX ZIX IZX ZZI XXZ YXY XYY YYZ [14] ZZZI
IIXX {3} ZII ZXX ZZZ ZYY IXX IYY IZZ XYY XZZ XXX XII [3] IIZZ
IXIX {5} YZY XZX IZI ZZZ YIY XIX ZIZ IXI ZXZ YXY XXX [5] IZIZ
XIIX {9} YYX ZXX XZX IIX XZI ZXI YYI IIZ XZZ ZXZ YYZ [9] ZIIZ
We can organize the 15 fano pencils and 15 fano planes in two doily’s, where a pencil and a plane share the same vertex if they share the same triple of the core of the MVL (figure 11).
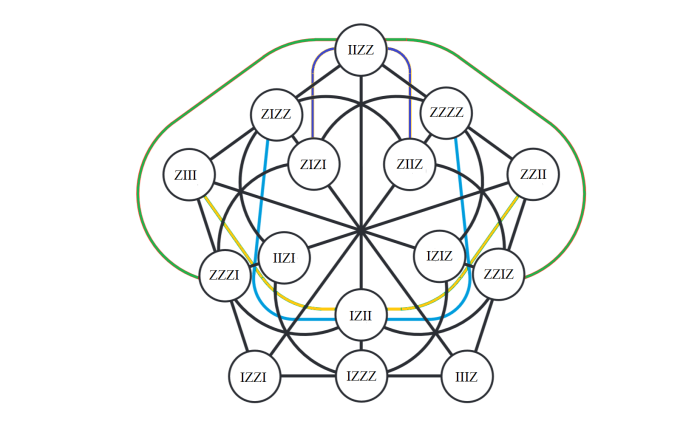
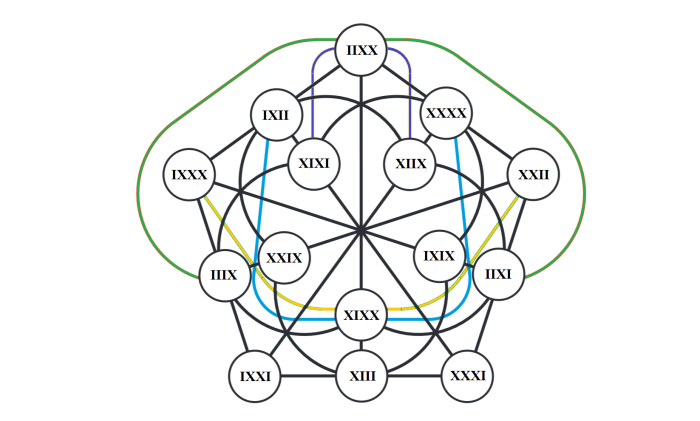
Or, use these two doily’s and the dictionary table in E8 section 15 .
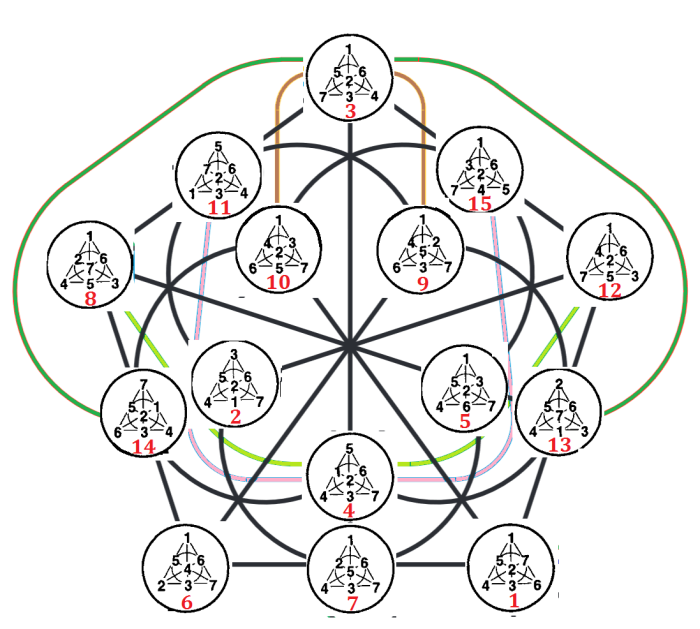
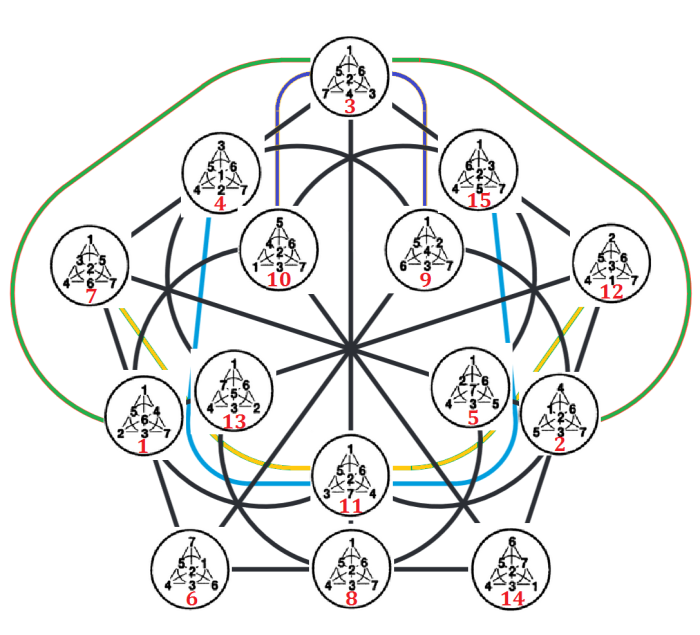
The three lines incident with 7 in each fano are from GQ 78 (the core doily in the MVL). The remaining four lines in each fano become, when translated to 3-qubit operators, the lines of the Mermin pentagrams. The conjugate pentagrams have their lines in the same 5 vertices of the two doily’s. To complete a pentagram, look for the 6 ovoids in the two doily’s and you find the double six of pentagrams with the combination of the 5 corresponding vertices.
GQ 78 admits another doily:
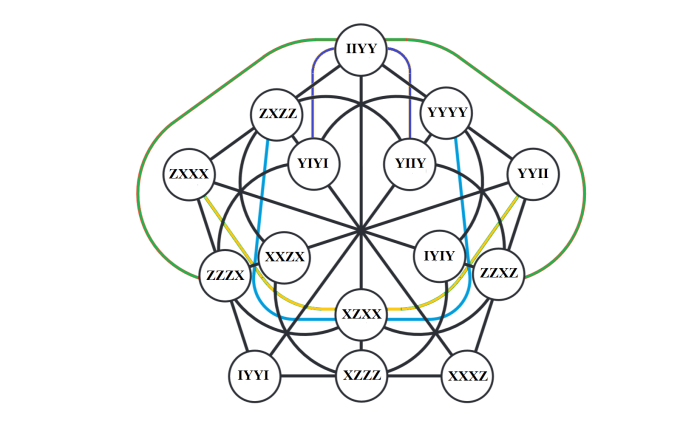
A vertex of the doily represents a fano plane that contains three lines of a flat pencil.
As example, take plane XXZX that shares three lines XIX, XZI and IZX of a flat pencil with plane XXIX and pencil IIZI. In figure 18 you see the dual with XIX, XZI and IZX as points:
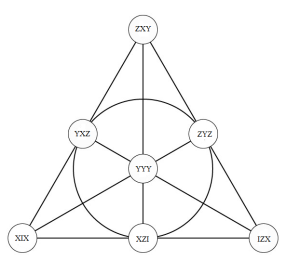
The other four points are in CYYY . The other 14 all contain YYY and the 3 other triples are easily found from the line of the core by multiplication with YYY.
XXXZ ↔ XIZ IXZ XXI YYY ZYX YZX ZZY
XXZX ↔ XIX XZI IZX YYY ZYZ ZXY YXZ
IIYY ↔ IXX IYY IZZ YYY YZZ YII YXX
XZXX ↔ ZIX IXX ZXI YYY XYZ YZZ XZY
IYIY ↔ YIY XIX ZIZ YYY IYI ZYZ XYX
IYYI ↔ YYI ZZI XXI YYY IIY XXY ZZY
XZZZ ↔ IXX XIX XXI YYY YZZ ZYZ ZZY
ZXXX ↔ IZZ ZIZ ZZI YYY YXX XYX XXY
YIIY ↔ XZI ZXI YYI YYY ZXY XZY IIY
YIYI ↔ XIZ ZIX YIY YYY ZYX XYZ IYI
ZXZZ ↔ XIZ IZZ XZI YYY ZYX YXX ZXY
YYII ↔ IZX IXZ IYY YYY YXZ YZX YII
ZZXZ ↔ ZIZ IXZ ZXI YYY XYX YZX XZY
ZZZX ↔ ZIX IZX ZZI YYY XYZ YXZ XXY
YYYY ↔YIY IYY YYI YYY IYI YII IIY
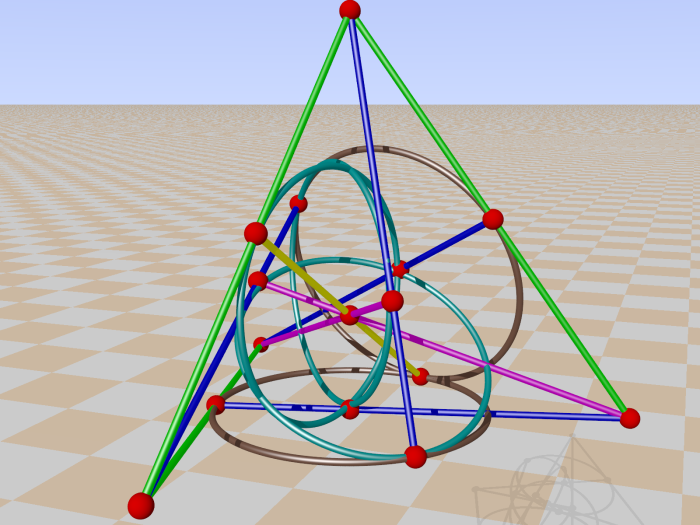
The 15 new triples are antisymmetric and commuting with YYY. They appear in the Witting polytope as a pair of the complex polytope 3{4}2 (red and orange) and a pair of the complex polytope 2{4}3 (green):
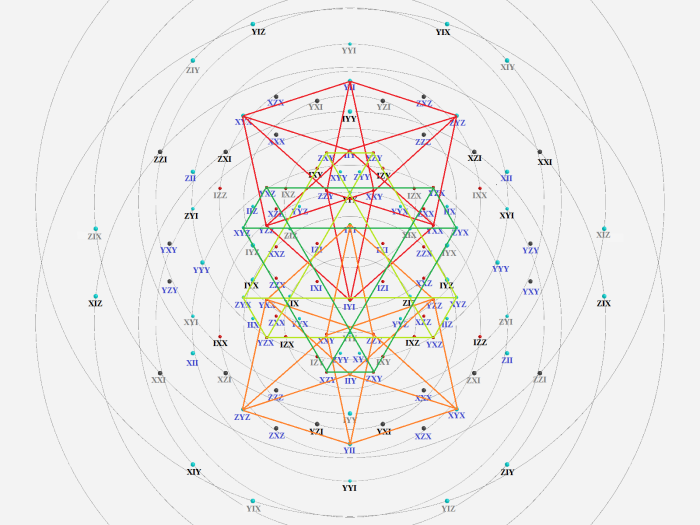
The split in these dual polytopes is reflected in the correspondence with a grid and its dual. A grid or GQ(2,1) has 9 points, incident with 2 lines, and 6 lines, incident with 3 points. A 3{4}2 has 9 vertices, incident with 2 triangular edges, and 6 triangular edges, incident with three vertices. But the triples of the edges are not commuting. We must choose the three diagonals and three triangular diameters for the six lines:
YII IYI IIY
YXX XYX XXY
YZZ ZYZ ZZY
YII YXX YZZ
IYI XYX ZYZ
IIY XXY ZZY
And dually… There is more to say about the Mermin squares in a separate page, but now return to the Mermin pentagrams.
The next picture shows a complex polytope 3{3}3 that we recognize as a line of a Mermin pentagram YYY IIY XXY ZZY.
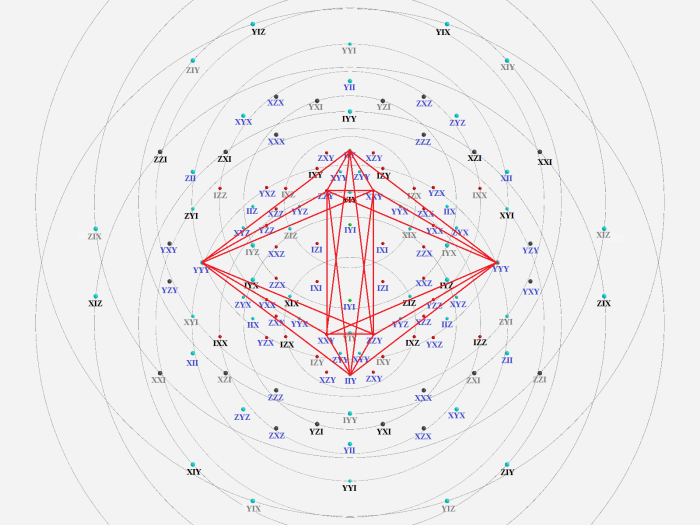
It is the complement of the line YYI ZZI XXI in the plane IYYI. This plane shows as:
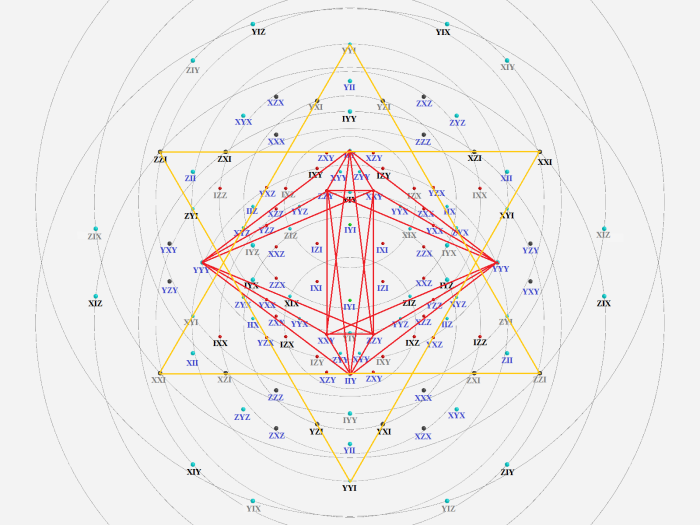
Then the plane IIYY with Mermin pentagram line YYY YII YXX YZZ as a 3{3}3:
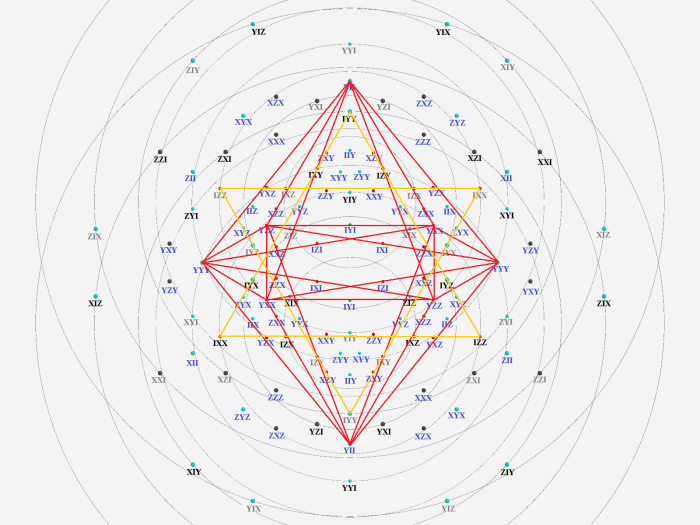
And a third one, plane IYIY:
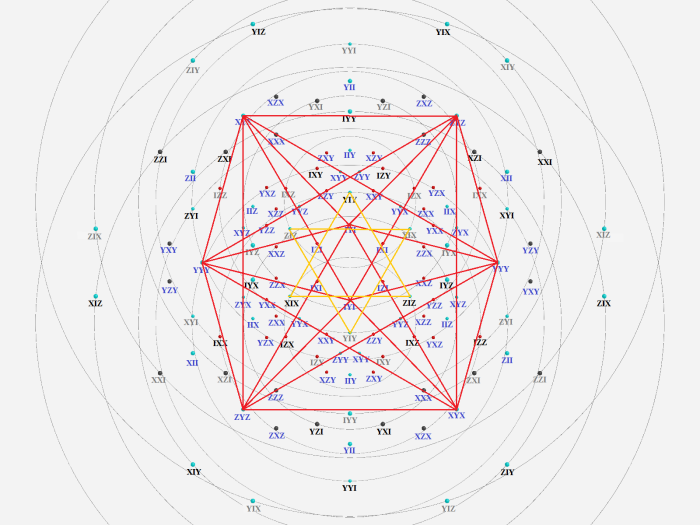
Plane YYYY is special with 6 points on a line:
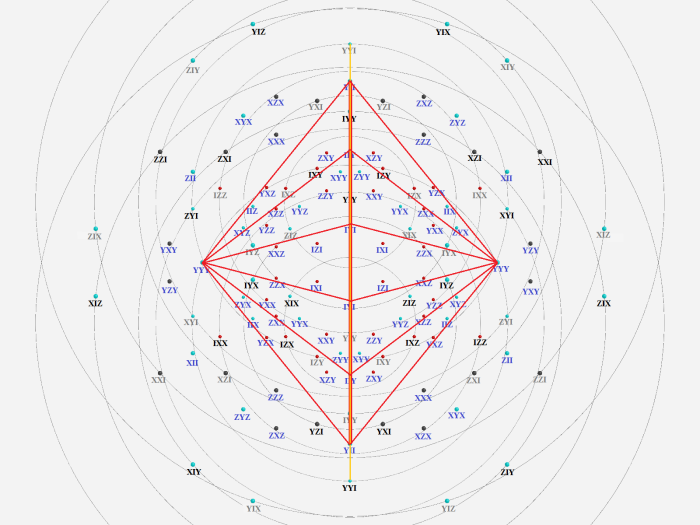
In the Witting polytope the lines of the conjugate Mermin pentagrams give the following pictures:
![Witting8b_54pt_72pts_IXYZ+++Mermin_conjugate_[3]+core.png](https://fgmarcelis.files.wordpress.com/2017/03/witting8b_54pt_72pts_ixyzmermin_conjugate_3core.png?w=700)
![Witting8b_54pt_72pts_IXYZ+++Mermin_conjugate_[5]+core.png](https://fgmarcelis.files.wordpress.com/2017/03/witting8b_54pt_72pts_ixyzmermin_conjugate_5core.png?w=700)
![Witting8b_54pt_72pts_IXYZ+++Mermin_conjugate_[6]+core](https://fgmarcelis.files.wordpress.com/2017/03/witting8b_54pt_72pts_ixyzmermin_conjugate_6core.png?w=700)
The other lines of the Mermin pentagrams are not related to complex polytopes, but yet to orthogonal vectors.
![Witting8b_54pt_72pts_IXYZ+++Mermin_conjugate_[12]+core.png](https://fgmarcelis.files.wordpress.com/2017/03/witting8b_54pt_72pts_ixyzmermin_conjugate_12core.png?w=700)
![Witting8b_54pt_72pts_IXYZ+++Mermin_conjugate_[15]+core.png](https://fgmarcelis.files.wordpress.com/2017/03/witting8b_54pt_72pts_ixyzmermin_conjugate_15core.png?w=700)
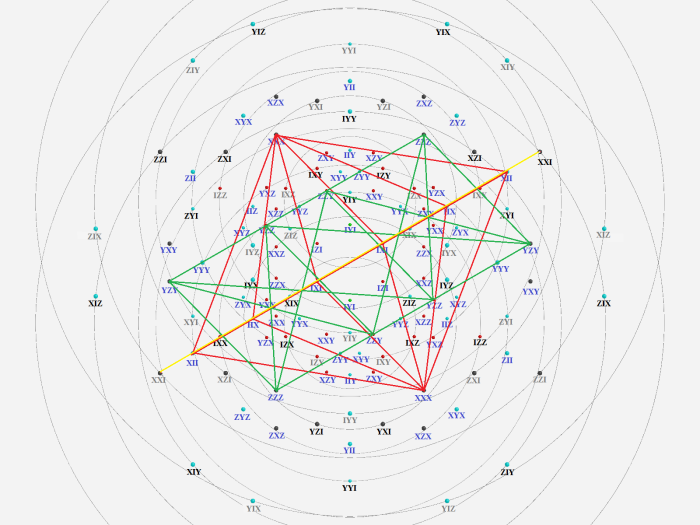
![Witting8b_54pt_72pts_IXYZ+++Mermin_conjugate_[2]+core2.png](https://fgmarcelis.files.wordpress.com/2017/03/witting8b_54pt_72pts_ixyzmermin_conjugate_2core2.png?w=700)
![Witting8b_54pt_72pts_IXYZ+++Mermin_conjugate_[13]+core2.png](https://fgmarcelis.files.wordpress.com/2017/03/witting8b_54pt_72pts_ixyzmermin_conjugate_13core2.png?w=700)
We can put the conjugate ones in determinant form as
ZZX XYY IXI
XII ZXZ YYX XXX
YXY IIX XZZ
XXZ ZYY IZI
ZII XZX YYZ ZZZ
YZY IIZ ZXX
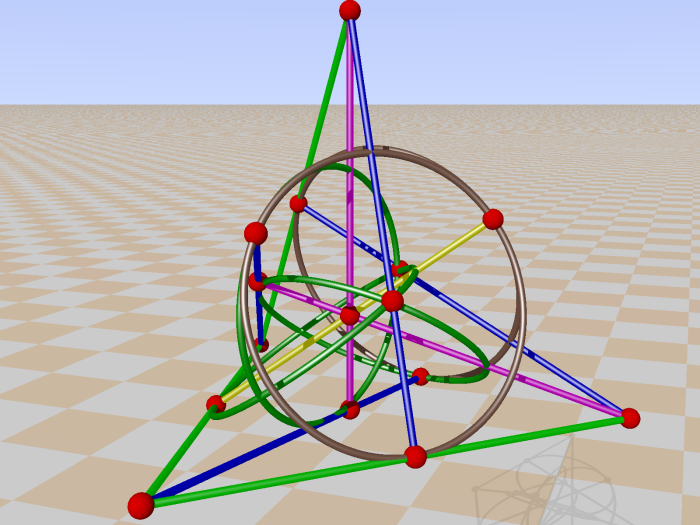
To see how many pentagrams there are we can make the doily belonging to GQ 68 :
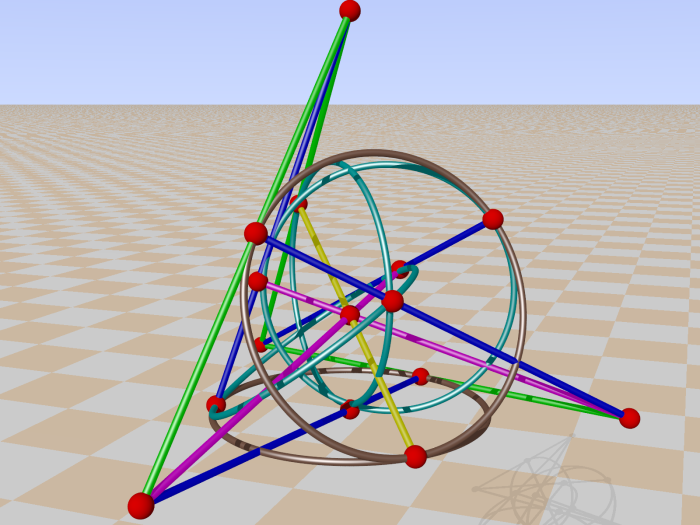
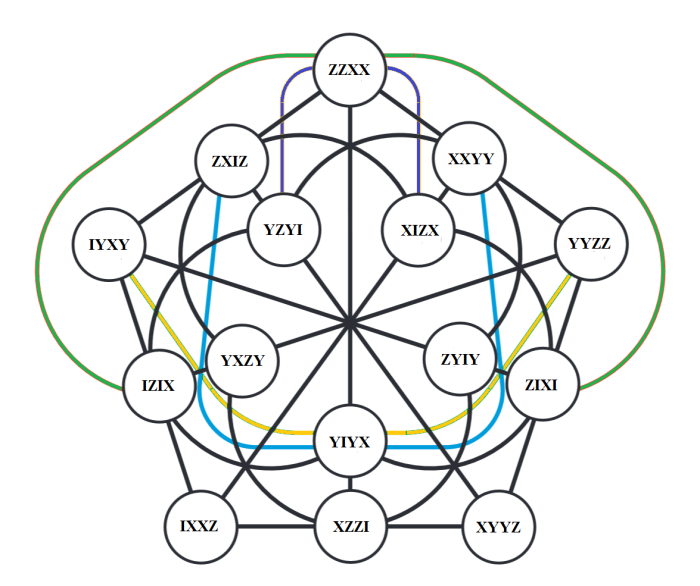
You can read the doily as follows: the set of 15 pencils are IIIZ, IIZI, IIZZ, …. , ZZZI, ZZZZ and the set of 15 planes IIIX, IIXI, …, XXXX . Using the trace map X→1, Z→1, Y→0, I→0, we get two sets of the numbers 1 to 15 in binary notation.
Take for example ZIXI and read this as flat pencil ZIII in plane IIXI, or flat pencil 8 (1000) in plane 2 (0010). . In the picture above the doily you can check that this is the case for two green lines and a blue line ( plane 2 is in point reperesentation 1-4-5-8-9-12-13). Second example: YYZZ is flat pencil 15 (ZZZZ) in plane 12 (XXII). Then ZZZZ•XXII = YYZZ. The two magenta lines and the yellow line in plane 12 (1-2-3-12-13-14-15).
Another GQ is GQ 18 :
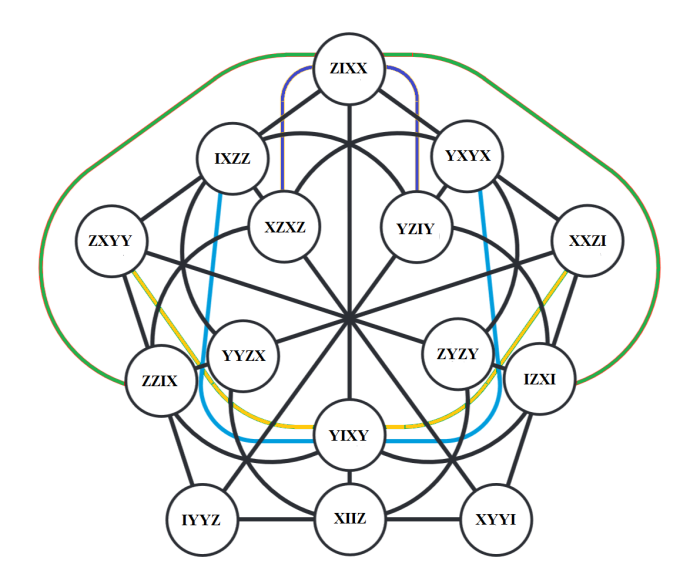
And GQ 28 :
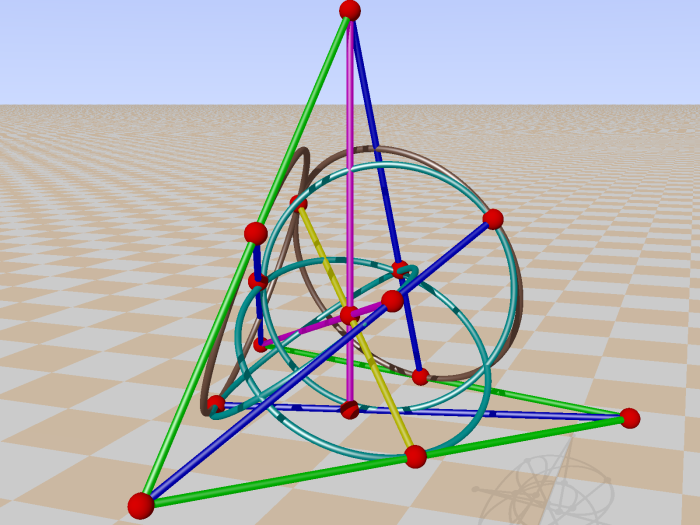
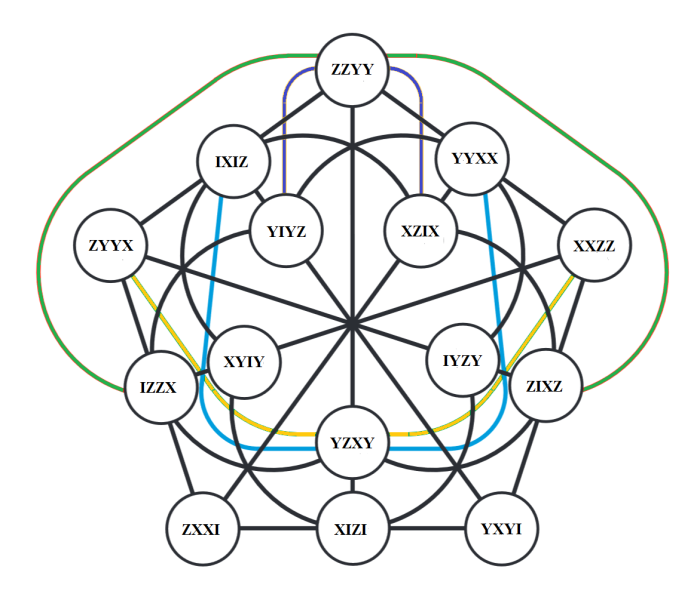
And GQ 38 :
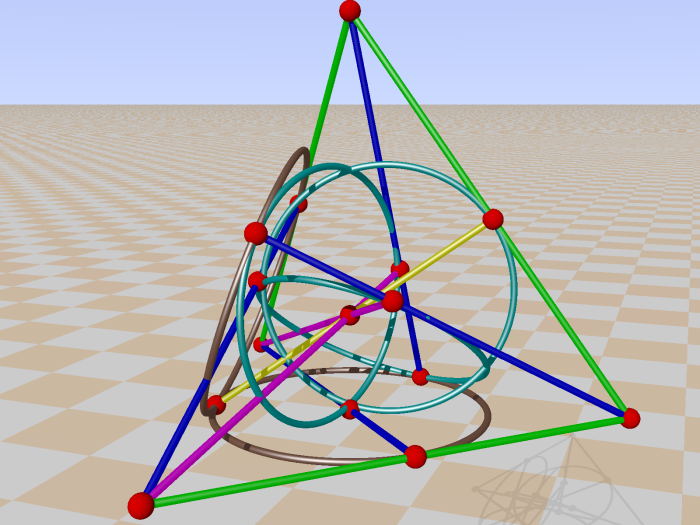
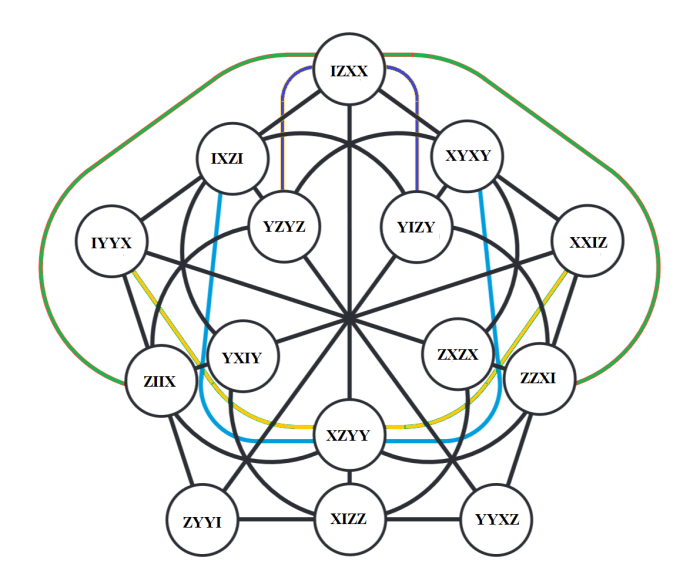
And GQ 48 :
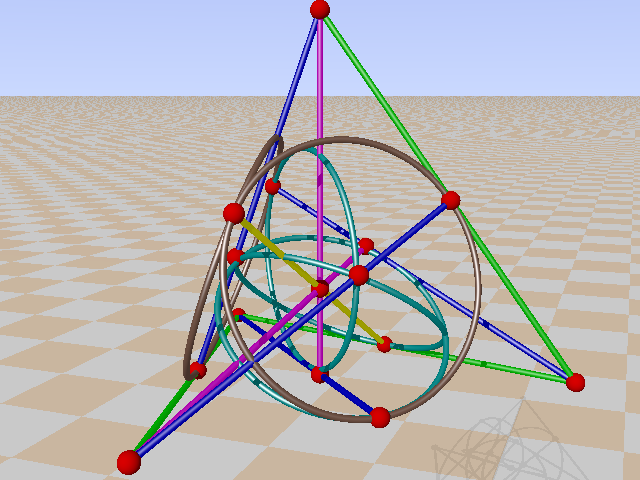
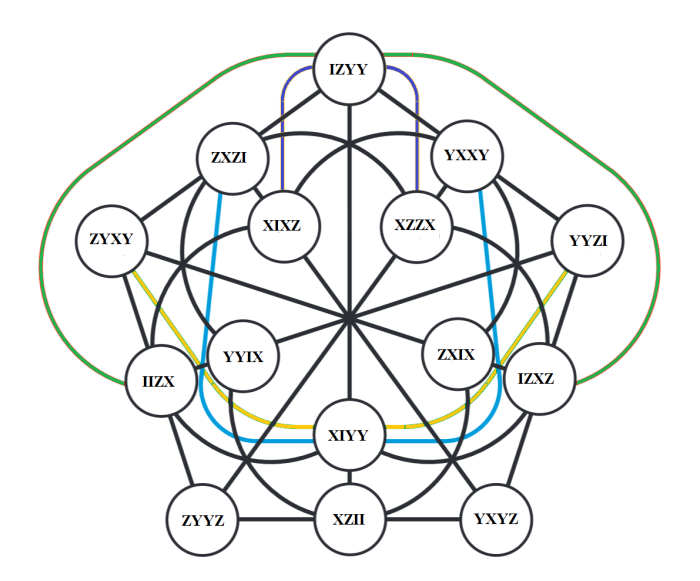
And GQ 58 :
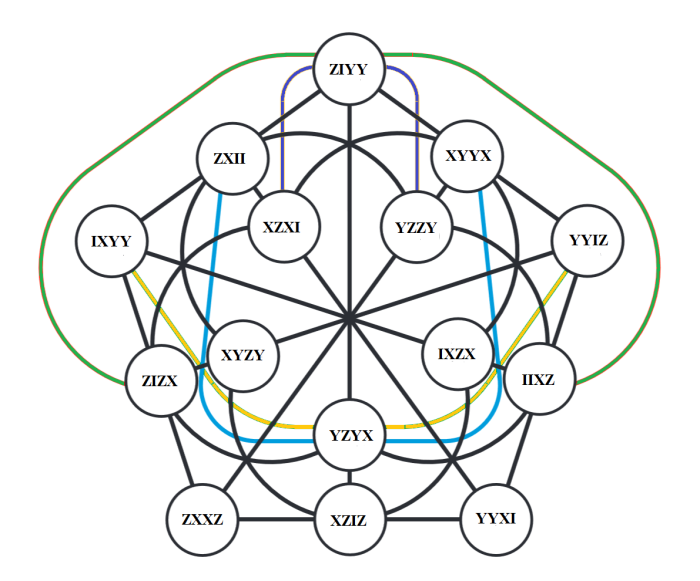
The nine PG(3,2)’s from FIGURE 13, 14, 17, 34, 36, 38, 40, 42 and 44 contain the 9×15 = 135 four qubit operators exactly once.
Seven PG(3,2)’s can be summarized in one :
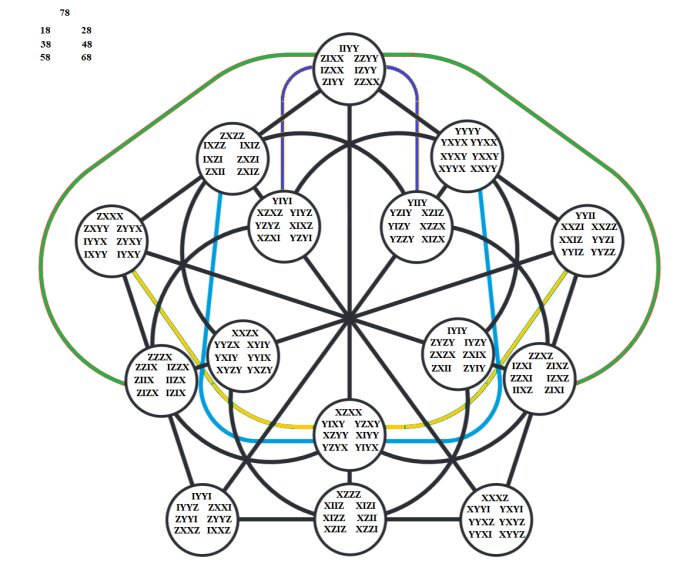
Compare this with FIGURE 16 where in the 15 Fano planes the 15×7 = 105 flat pencils can be recognized in the same vertex. Operators belonging to the same PG(3,2) can be found in the same relative postion within a vertex, indicated in FIGURE 45 in the left upper corner. The 15 planes and 15 full pencils are easily deduced from 78 . For instance IIYY hints to IIXX and IIZZ, and ZXZZ hints to ZIZZ and IXII. In this way FIGURE 45 summarizes the 135 symmetric operators.